| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 딕셔너리
- 재귀함수
- 데이터분석
- 파이썬
- 추천시스템
- 사이킷런
- 코딩도장
- 스크랩
- Set
- AI
- Python
- 딥러닝
- 카카오
- 후기
- 제로베이스 데이터사이언스
- NLP
- 머신러닝
- 클래스
- TensorFlow
- 함수
- 데이터사이언스 스쿨
- numpy
- 데이터사이언티스트
- AIFFEL
- 파이썬코딩도장
- 아이펠
- 자연어처리
- 제어문
- 기사
- 속성
- Today
- Total
뮤트 개발일지
AIFFEL 아이펠 22일차 본문
비지도학습
비지도학습 Unsupervised learning: 지도학습과 달리 training data로 정답label이 없는 데이터가 주어지는 학습방법. 주어진 데이터가 어떻게 구성되어 있는지 스스로 알아내는 방법이라고 할 수 있다.
클러스터링(군집화)
명확한 기준이 없는 상황에서 데이터들을 분석하여 가까운(또는 유사한) 것들끼리 묶어주는 작업
그 방법으로는 아래와 같은 것들이 있다.
K-means
k 값이 주어졌을 때, 데이터들을 k개의 클러스터로 묶는 알고리즘
코드로 보자면,
%matplotlib inline
from sklearn.datasets import make_blobs
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random
# 중심점이 5개인 100개의 점 데이터를 무작위로 생성
points, labels = make_blobs(n_samples=100, centers=5, n_features=2, random_state=135)
print(points.shape, points[:10]) # 무작위로 생성된 점의 좌표 10개 출력
print(labels.shape, labels[:10]) # 10개의 점들이 각각 대응하는 중심점(label) 값 출력
>>>
(100, 2) [[ 4.63411914 -6.52590383]
[-6.52008604 7.16624288]
[ 2.14142339 -5.21092623]
[ 1.70054231 8.54077897]
[-0.33809159 8.76509668]
[-7.69329744 7.94546313]
[ 3.89090121 -3.06531839]
[ 3.22338498 -2.93209009]
[-6.63962964 5.34777334]
[ 6.37904965 -6.46617328]]
(100,) [2 1 0 3 3 1 0 0 1 2]임의로 지정한 k개의 중심점이 새로운 label 역할을 한다.
좌표에 그려보자.
# 축 그리기
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
# 위에서 생성한 점 데이터들을 pandas DataFrame 형태로 변환하기
points_df = pd.DataFrame(points, columns=['X', 'Y'])
display(points_df.head())
# 점 데이터를 X-Y grid에 시각화하기
ax.scatter(points[:, 0], points[:, 1], c='black', label='random generated data')
# 축 이름을 라벨에 달고, 점 데이터 그리기
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.legend()
ax.grid()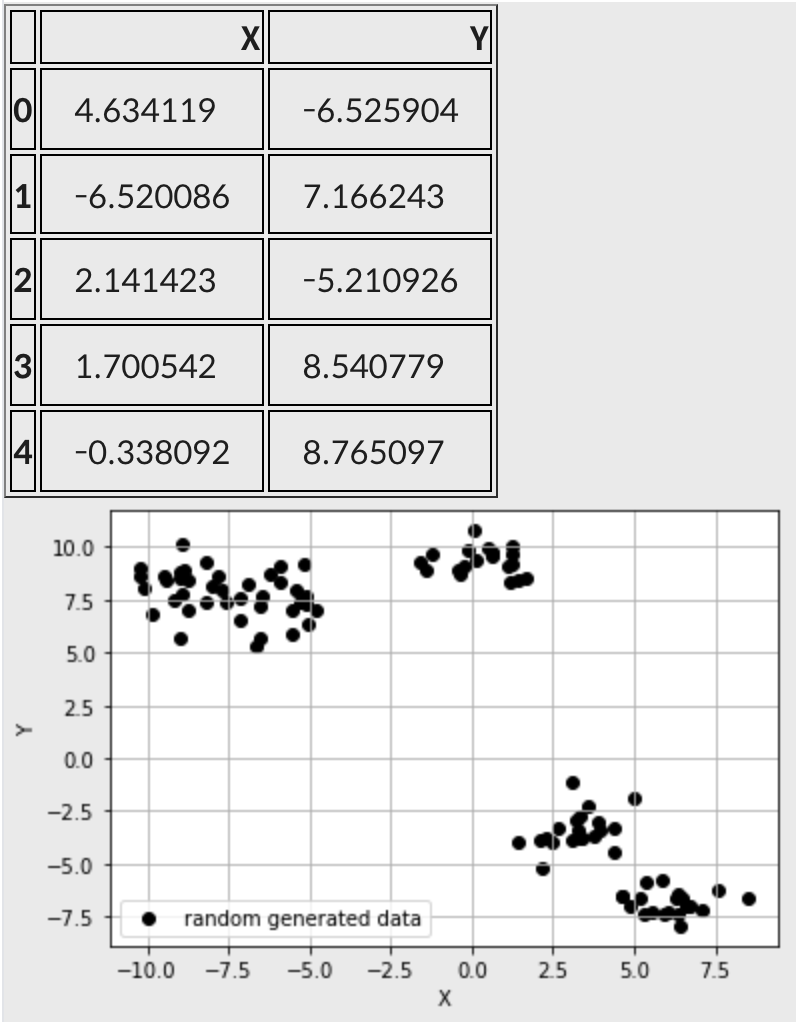
생성한 데이터에 k-means를 적용해보자.
알고리즘을 적용하는 순서)
1. 원하는 클러스터의 수K를 결정한다.
2. 무작위로 클러스터의 수와 같은 K개의 중심점centroid을 선정한다. 이들은 각각의 클러스터를 대표한다.
3. 나머지 점들과 모든 중심점 간의 *유클리드 거리를 계산한 후, 가장 가까운 거리를 가지는 중심점의 클러스터에 속하도록 한다.
4. 각 K개의 클러스의 중심점을 재조정한다. 특정 클러스터에 속하는 모든 점들의 편균값이 해당 클러스터 다음 iteration의 중심점이 된다.
(이 중심점은 실제로 존재하는 데이터가 아니어도 된다.)
5. 재조정된 중심점을 바탕으로 모든 점들과 새로 조정된 중심점 간의 유클리드 거리를 다시 계산한 후, 가장 가까운 거리를 갖는 클러스터에 해당 점을 재배정한다.
6. 4번과 5번을 반복 수행한다. 반복 횟수는 사용자가 조절하고, 특정 iteration 이상이 되면 수렴(중심점이 더이상 바뀌지 않음)하게 된다.
* 위에서 나온 유클리드 거리란...
http://egloos.zum.com/metashower/v/9957577
데이터 분석에서 나오는 수학 - 유클리디안 거리
유클리디안 거리 아래 그림에서 초록색 이 유클리드 거리이다. 유클리디안 거리는 유클리드라는 수학자가 고안해낸 이론이다. 최대공약수를 계산하는 유클리드 호제법으로 유명한 분이다. 유
egloos.zum.com
코드로 확인해보자.
from sklearn.cluster import KMeans
# 1), 2) 위에서 생성한 무작위 점 데이터(points)에 클러스터의 수(K)가 5인 K-means 알고리즘을 적용
kmeans_cluster = KMeans(n_clusters=5)
# 3) ~ 6) 과정이 전부 함축되어 있는 코드. points에 대하여 K가 5일 때의 K-means iteration을 수행
kmeans_cluster.fit(points)
print(type(kmeans_cluster.labels_))
print(np.shape(kmeans_cluster.labels_))
print(np.unique(kmeans_cluster.labels_))
>>>
<class 'numpy.ndarray'>
(100,)
[0 1 2 3 4]시각화 해보면,
# n 번째 클러스터 데이터를 어떤 색으로 도식할 지 결정하는 color dictionary
color_dict = {0: 'red', 1: 'blue', 2:'green', 3:'brown', 4:'indigo'}
# 점 데이터를 X-Y grid에 시각화
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
# K-means clustering의 결과대로 색깔별로 구분하여 점에 색칠한 후 도식
for cluster in range(5):
cluster_sub_points = points[kmeans_cluster.labels_ == cluster] # 전체 무작위 점 데이터에서 K-means 알고리즘에 의해 군집화된 sub data를 분리합니다.
ax.scatter(cluster_sub_points[:, 0], cluster_sub_points[:, 1], c=color_dict[cluster], label='cluster_{}'.format(cluster)) # 해당 sub data를 plot합니다.
# 축 이름을 라벨에 달고, 점 데이터 그리기
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.legend()
ax.grid()
그러나 K-means가 동작하지 않는 경우도 있다.
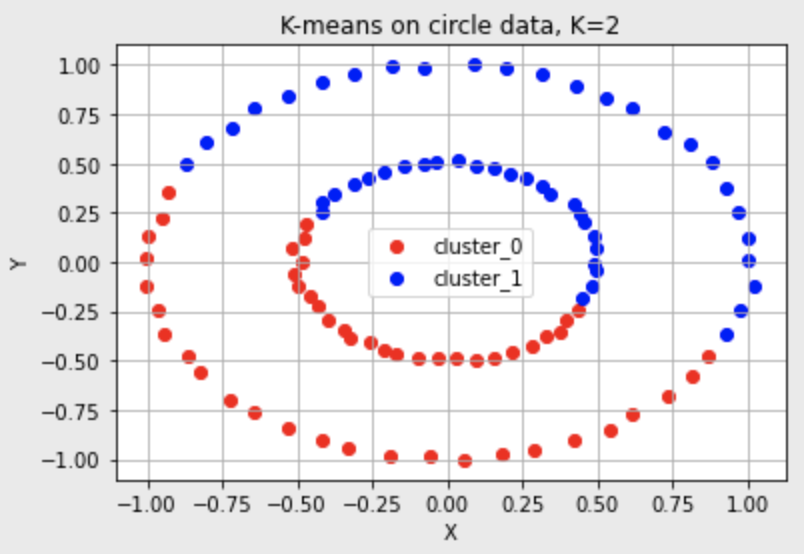
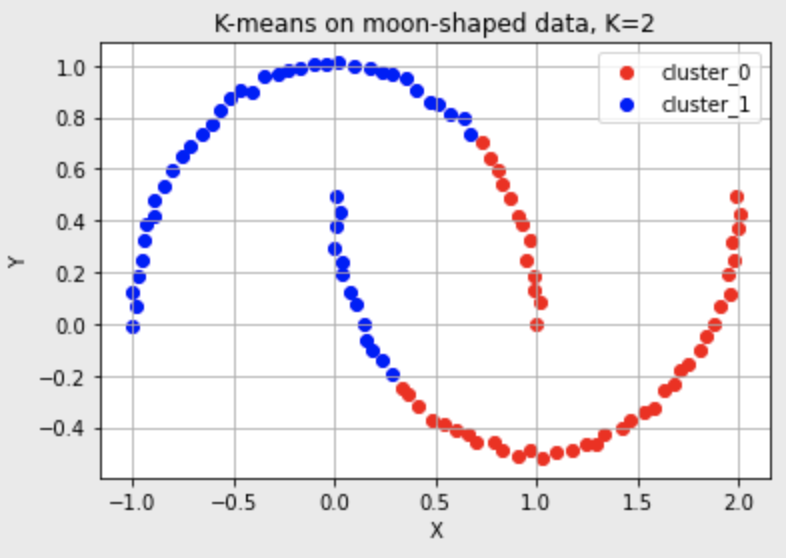
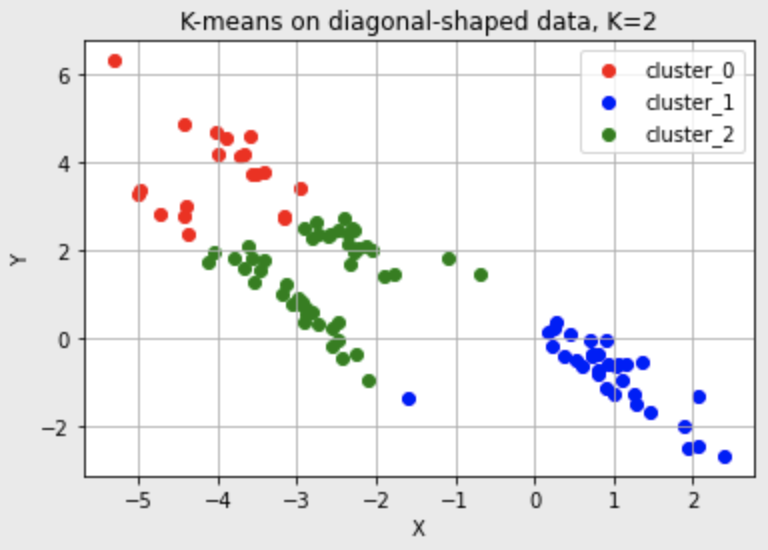
K-means의 한계
군집의 개수K를 미리 지정해야 하기 때문에 이를 알거나 예측하기 어려운 경우에는 사용하기 어렵다.
유클리드 거리가 가까운 데이터끼리 군집이 형성되기 때문에 데이터의 분포에 따라 유클리드 거리가 멀면서 밀접하게 연관되어 있는 데이터들의 군집화를 성공적으로 수행하지 못할 수 있다.
이러한 한계를 극복하기 위한 방법으로는,(군집의 개수를 명시하지 않으면서 밀도 기반으로 군집을 예측하는 방법)
DBSCAN (Density Based Spatial Clustering of Applications with Noise)
밀도 기반의 군집 알고리즘이다. 군집의 개수를 미리 지정할 필요가 없으며 거리 기반이 아닌 밀도 있게 몰려 있는 클러스터를 군집화하는 방식으로 사용하기 때문에 불특정한 형태의 군집도 찾을 수 있다.
이해를 돕는 시각화 자료...
http://primo.ai/index.php?title=Density-Based_Spatial_Clustering_of_Applications_with_Noise_(DBSCAN)
Density-Based Spatial Clustering of Applications with Noise (DBSCAN) - PRIMO.ai
Helpful resources for your journey with artificial intelligence; videos, articles, techniques, courses, profiles, and tools
primo.ai
용어 설명)
- epsilon: 클러스터의 반경
- minPts: 클러스터를 이루는 개체의 최소값
- core point: 반경 epsilon 내에 minPts개 이상의 점이 존재하는 중심점
- border point: 군집의 중심이 되지는 못하지만 군집에 속하는 점
- noise point: 군집에 포함되지 못하는 점
알고리즘을 적용하는 순서)
1. 임의의 점p 설정, p를 포함하여 주어진 elipson 안에 포함되어 있는 점들의 개수를 센다.
2. 해당 원에 minPts개 이상의 점이 포함되어 있으면, 해당 점p를 core point로 간주하고 원에 포함된 점들을 하나의 클러스터로 묶는다.
3. 해당 원에 minPts 개 미안의 점이 포함되어 있으면 일단 pass한다.
4. 모든 점에 대하여 돌아가면서 1~3번의 과정을 반복한다. 만일 새로운 점p'가 core point가 되고 이 점이 기존의 클러스터에 속한다면, 두 개의 클러스터는 연결되어 있다고 판단하며 하나의 클러스터로 묶는다.
5. 모든 점에 대하여 클러스터링을 끝냈는데, 어떤 점을 중심으로 하더라도 클러스터에 속하지 않는 점이 있다는 이를 noise point로 간주한다. 또한 특정 군집에는 속하지만 core point가 아닌 점들을 border point라고 칭한다.
DBSCAN 알고리즘 적용하기
K-means에서 안됐던 예시를 적용해보자. (예시 중 원형 모델만 코드로 구현)
# DBSCAN으로 circle, moon, diagonal shaped data를 군집화한 결과
from sklearn.cluster import DBSCAN
fig = plt.figure()
ax= fig.add_subplot(1, 1, 1)
color_dict = {0: 'red', 1: 'blue', 2: 'green', 3:'brown',4:'purple'} # n 번째 클러스터 데이터를 어떤 색으로 도식할 지 결정하는 color dictionary
# 원형 분포 데이터 plot
epsilon, minPts = 0.2, 3 # 2)와 3) 과정에서 사용할 epsilon, minPts 값을 설정
circle_dbscan = DBSCAN(eps=epsilon, min_samples=minPts) # 위에서 생성한 원형 분포 데이터에 DBSCAN setting
circle_dbscan.fit(circle_points) # 3) ~ 5) 과정을 반복
n_cluster = max(circle_dbscan.labels_)+1 # 3) ~5) 과정의 반복으로 클러스터의 수 도출
print(f'# of cluster: {n_cluster}')
print(f'DBSCAN Y-hat: {circle_dbscan.labels_}')
# DBSCAN 알고리즘의 수행결과로 도출된 클러스터의 수를 기반으로 색깔별로 구분하여 점에 색칠한 후 도식
for cluster in range(n_cluster):
cluster_sub_points = circle_points[circle_dbscan.labels_ == cluster]
ax.scatter(cluster_sub_points[:, 0], cluster_sub_points[:, 1], c=color_dict[cluster], label='cluster_{}'.format(cluster))
ax.set_title('DBSCAN on circle data')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.legend()
ax.grid()
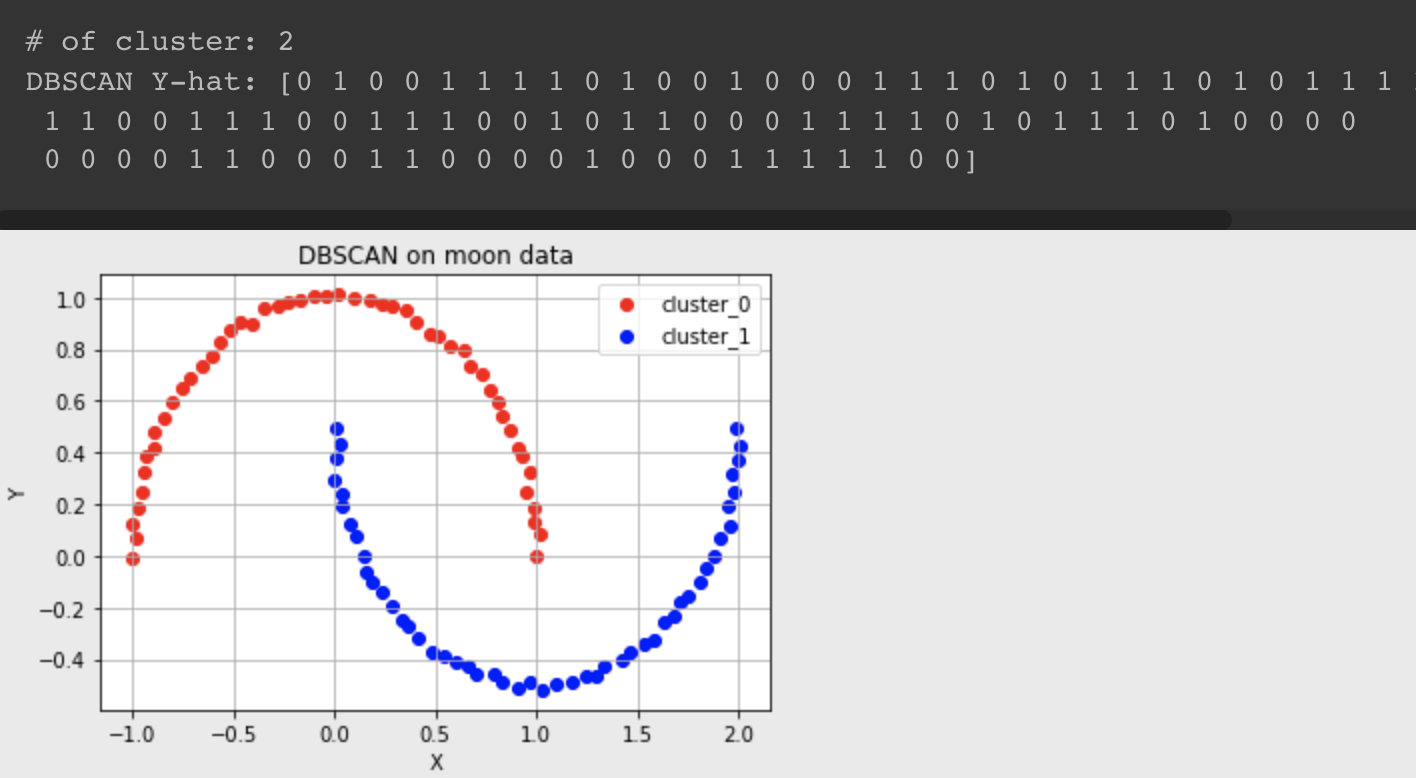
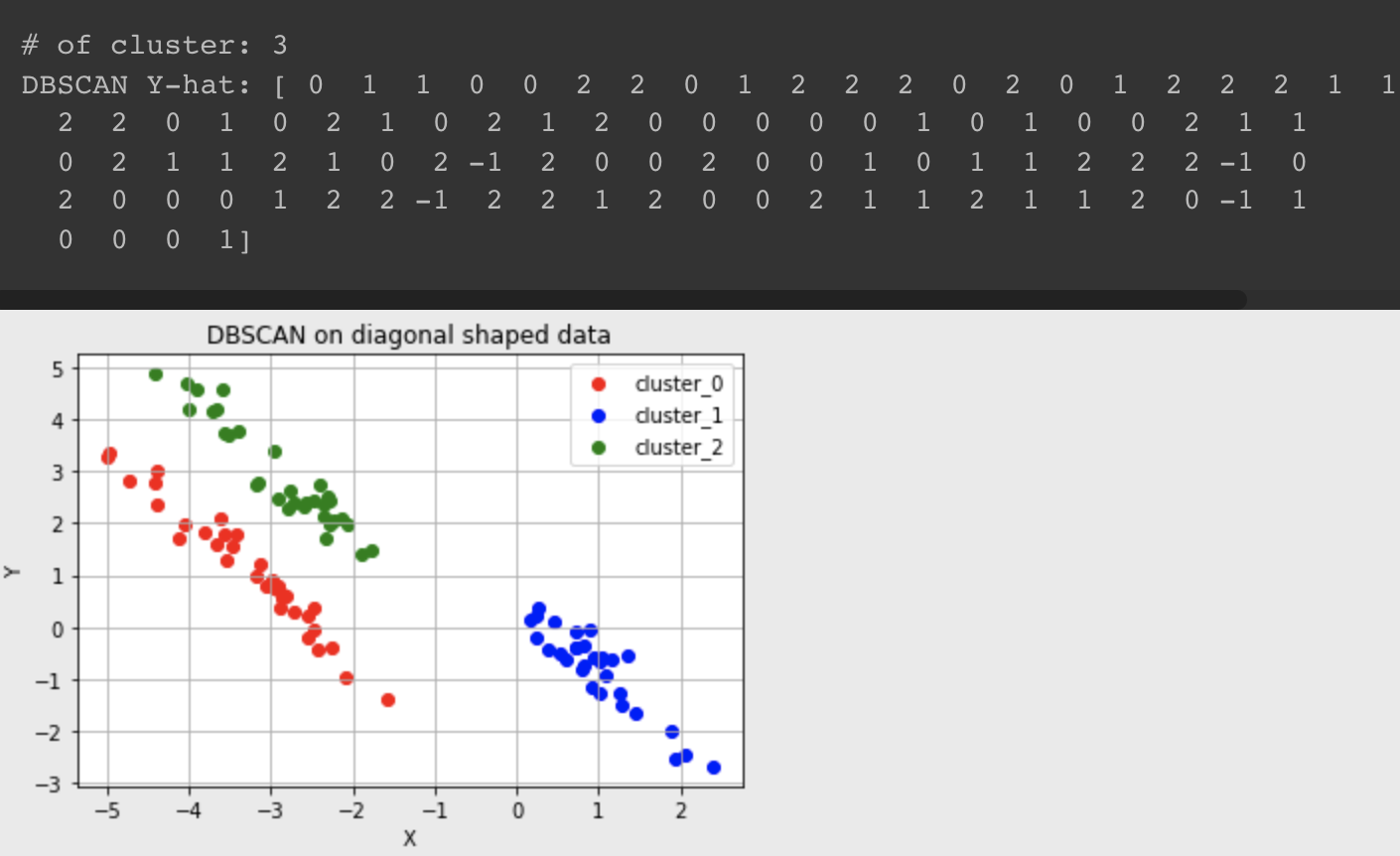
Y-hat이 -1인 경우는 noise point로 된 것!
DBSCAN의 한계
데이터가 많을수록 DBSCAN의 알고리즘 수행 시간이 급격하게 늘어난다.
클러스터의 수를 지정해줄 필요는 없으나, 데이터 분포에 맞는 epsilon과 minPts의 값을 지정해 주어야 한다.
차원 축소
PCA
비지도학습에서 데이터를 나타내느 여러 특징feature들 중에서 어떤 특징이 가장 그 데이터를 잘 표현represent하는지 알게 해주는 특징 추출feature extraction의 용도로 사용된다.
PCA를 이해하기 위해서는 선형대수 지식이 필요하다.
=>
PCA는 데이퍼 분포의 주성분을 찾아주는 방법이다.
주성분: 데이터의 분산이 가장 큰 방향 벡터
PCA는 데이터들의 분산을 최대로 보존하면서, 서로 직교orthogonal하는 기저basis들을 찾아 고차원 공간을 저차원 공간으로 사영projection한다.(후우 무슨 말이냐.. 하나씩 뜯어보자)
또한 PCA에서는 기존 특성 중 중요한 것을 선택하는 방식이 아닌 기존의 특성을 선형 결합linear combination하는 방식을 사용한다.

위 그림에서 보이는 우상향의 긴 화살표와 좌상향의 짧은 화살표를 새로운 좌표축으로 삼을 수 있을 것이다. 이렇게 새로운 좌표계 역할을 할 수 있는 벡터의 모음을 기저basis라고 한다.
차원의 수는 줄이면서, 데이터 분포의 분산을 최대한 유지하기 위해,
가장 분산이 긴 축을 첫 기저로 잡고, 그 기저에 직교하는 축 중 가장 분산이 큰 값을 다음 기저로 잡는다.
이 과정을 반복하면 차원의 수를 최대로 줄이면서 데이터 분포의 분산을 유지할 수 있다. 이것이 차원축소!
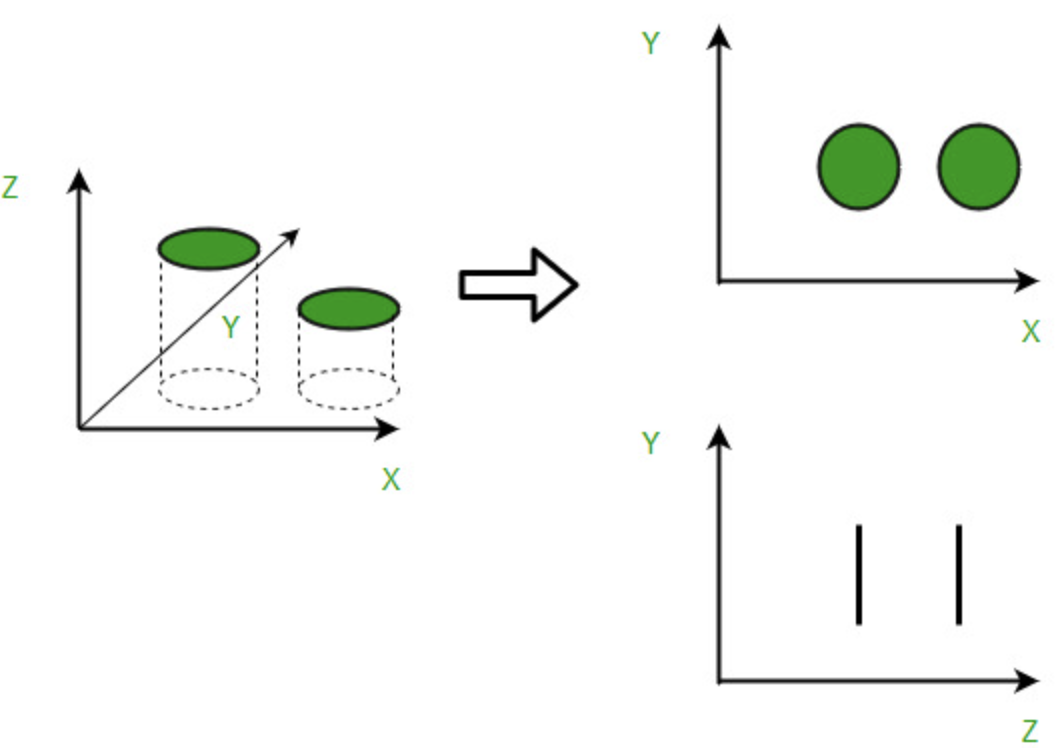
X-Y-Z 좌표축 상에 존재하는 데이터를 X-Y, Y-Z 좌표축에 사영projection했다는 것: 각각 Z, X좌표축을 무시했다는 뜻
그러면 무시한 데이터만큼의 정보 손실이 일어난다. 위 그림에서 원본 데이터의 특성을 상대적으로 잘 살리면서 차원을 1개 축소한 것은 X-Y이다. 그렇다면 Z축 방향의 정보는 상대적으로 덜 중요하다고 할 수 있다. 수학적으로 이를 Z축 방향의 분산이 적다고 한다.
PCA는 차원축소를 시도하되, 주어진 좌표축 방향이 아니라, 가장 분산이 길게 나오는 기저 방향을 찾아 그 방향의 기저만 남기고, 덜 중요한 기저 방향을 삭제하는 방식으로 진행된다. 이렇게 찾은 가장 중요한 기저를 주성분Principal Component 방향, 또는 pc축이라고 한다.
===> PCA는 각 feature간 상관관계가 있고 이를 추릴 필요가 있을 때 유용하게 사용되는 비지도학습 방법 중 하나이다.
T-SNE(T-Stochastic Neighbor Embedding)
시각화에 많이 쓰이는 알고리즘

위 이미지처럼 방사형적, 비선형적 데이터에서는 주성분으로 잡을 선형적인 축을 찾기 어렵다. 위 데이터를 PCA를 이용해 2차원으로 표현하면, 멀리있는 데이터가 가까이 있도록 차원축소가 이뤄지게 된다.
T-SNE는 기존 차원의 공간에서 가까운 점들은 차원축소된 공간에서도 여전히 가깝게 유지되는 것을 목표로 한다.
MNIST 데이터로 PCA와 T-SNE 결과 비교
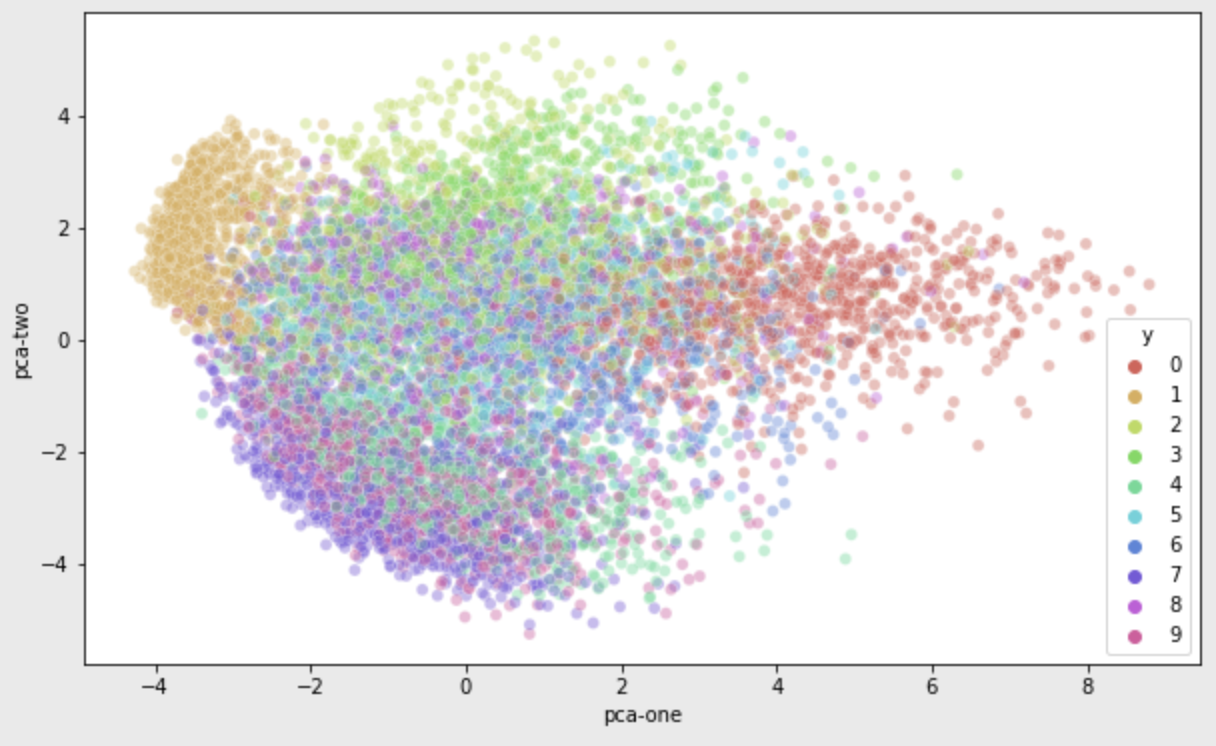
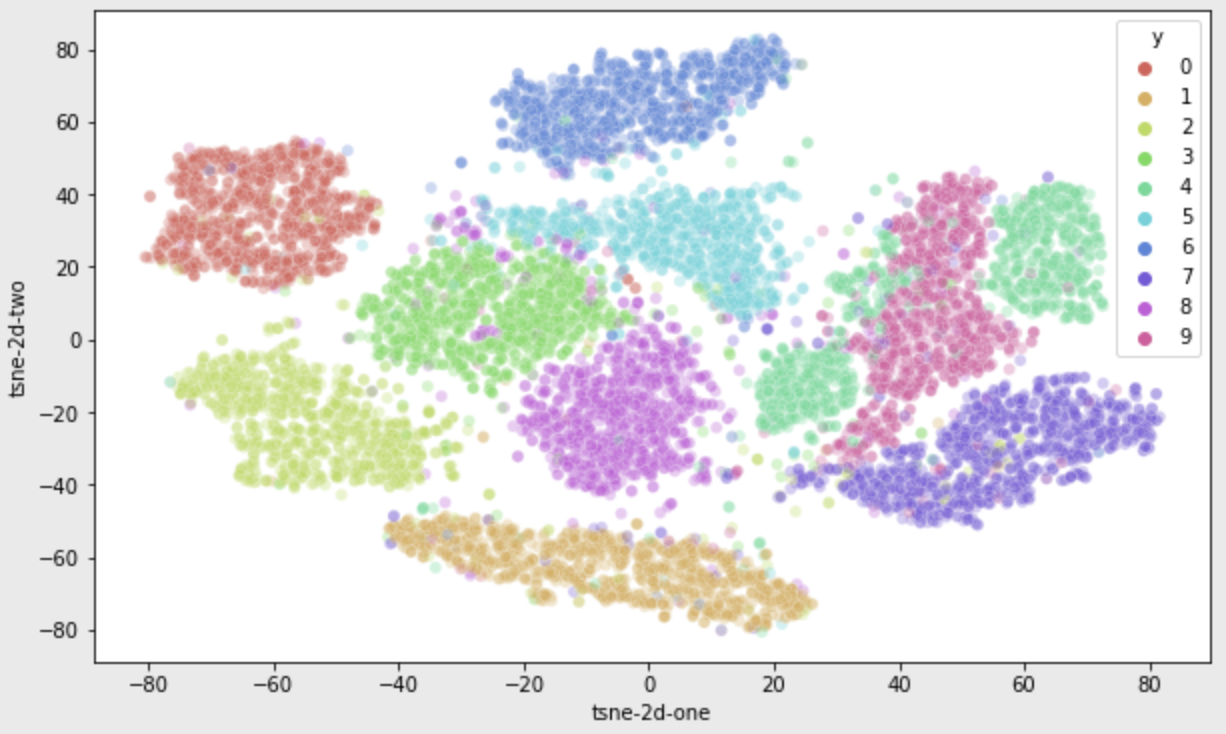
그렇다면 T-SNE는 PCA보다 우월한 차원축소 기법일까? No!
T-SNE의 두 차원은 물리적 의미를 갖지 않는다. PCA는 정보 손실을 최소화하려는 관점을 갖고 있으므로, 그 결과 추출된 pc축은 주성분이라는 물리적 의미를 유지하고 있고, 공분산을 통해 원본 데이터를 일정 부분 복원할 수 있는 가능성이 있다.
그러나 T-SNE는 정보 손실량에 주목하지 않으며, 그 결과 저차원 축이 아무런 물리적 의미를 갖지 못한다. 오직 시각화에만 유리할 뿐

음... 그래도 차원축소는 이해가 안 간다..ㅜ
mnist 데이터 분석한 코드를 다시 보면서 이해해보고 싶은데 시간이 부족부족해...
'AIFFEL' 카테고리의 다른 글
| AIFFEL 아이펠 24일차 (0) | 2022.02.03 |
|---|---|
| AIFFEL 아이펠 23일차 (0) | 2022.02.03 |
| AIFFEL 아이펠 21일차 (1) | 2022.01.26 |
| AIFFEL 아이펠 20일차 (0) | 2022.01.25 |
| AIFFEL 아이펠 19일차 (0) | 2022.01.25 |


